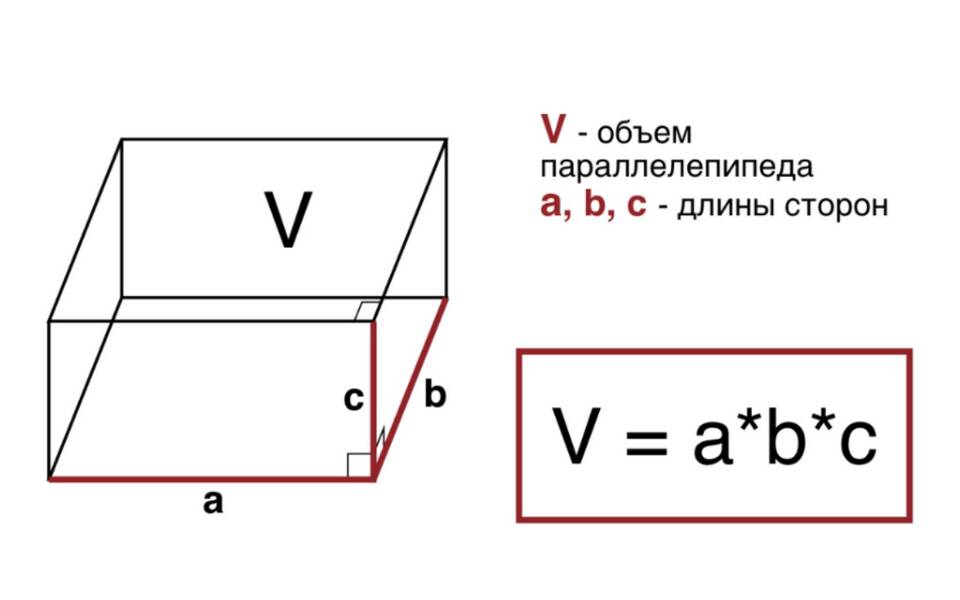
Прямоугольный параллелепипед - это трехмерная фигура, все грани которой являются прямоугольниками. В таком параллелепипеде существует несколько типов диагоналей, каждая из которых имеет свои особенности вычисления.
Содержание
Виды диагоналей в прямоугольном параллелепипеде
| Граневые диагонали | Диагонали боковых граней |
| Пространственные диагонали | Диагонали, соединяющие противоположные вершины |
Формулы для вычисления диагоналей
- Граневая диагональ: d = √(a² + b²), где a и b - стороны грани
- Пространственная диагональ: D = √(a² + b² + c²), где a, b, c - измерения параллелепипеда
Вычисление суммы всех диагоналей
В прямоугольном параллелепипеде с измерениями a, b, c:
- Имеется 12 граневых диагоналей (по 4 на каждую пару измерений)
- Имеется 4 пространственных диагонали
- Общая сумма всех диагоналей вычисляется по формуле: S = 4(√(a²+b²) + √(a²+c²) + √(b²+c²)) + 4√(a²+b²+c²)
Пример расчета
| Размеры | a=3, b=4, c=5 |
| Граневые диагонали | 4(5 + √34 + √41) ≈ 4(5 + 5,83 + 6,40) ≈ 68,92 |
| Пространственные диагонали | 4√50 ≈ 4×7,07 ≈ 28,28 |
| Общая сумма | ≈ 97,20 |
Особенности вычислений
- Сумма диагоналей зависит от всех трех измерений параллелепипеда
- Для куба (a=b=c) формула упрощается: S = 12a√2 + 4a√3
- Значение имеет практическое применение в строительстве и проектировании
Точное вычисление суммы диагоналей прямоугольного параллелепипеда требует последовательного применения соответствующих формул и учета всех составляющих.